


Next: Estimating in the the
Up: Lookpainting: Towards developing a
Previous: Mathematical framework for lookpainting:
In situations where the image data is extremely noisy,
and/or where a closed-form solution for f(q) is desired,
a parametric method is used, in which a function g(f)that is the range-range function
of a suitable response function f(q) is selected.
The method amounts to a curve fitting problem
in which the parameters of g are selected so that
g best fits one or more joint histograms constructed from
two or more differently exposed spatially registered
images under analysis.
Various parametric models have
been considered for this purpose [12].
For example, the one parameter model,
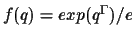 is equivalent to applying gamma correction
is equivalent to applying gamma correction
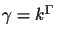 to f in order to obtain
to f in order to obtain
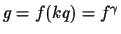 ,
where
,
where 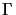 is typically between 0 and 1/2.
Note that when tonally registering images using this gamma correction,
one makes an implicit assumption that f(q) does not go all
the way to zero when q=0.
Thus a better model is
f=exp((1+qb)c) which also nicely captures the toe and shoulder of the
response function.
is typically between 0 and 1/2.
Note that when tonally registering images using this gamma correction,
one makes an implicit assumption that f(q) does not go all
the way to zero when q=0.
Thus a better model is
f=exp((1+qb)c) which also nicely captures the toe and shoulder of the
response function.
However, one of the simplest models from a parameter estimation point of view
is the classic response curve,
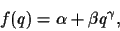 |
(8) |
used by photographers to characterize the response of a variety of
photographic emulsions (and suitable also to characterize the response
of electronic imaging devices which attempt to emulate the appearance
of film), including so-called extended response
film[15].
Proposition 3.2
The comparametric plot corresponding to
the standard photographic response
function (
8) is a straight line.
The slope is
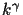
,
and the
intercept is
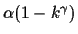
.
Proof:
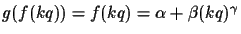
Re-arranging to eliminate
q gives
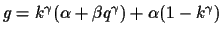
so that:
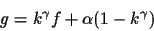 |
(9) |
This result suggests that f(q) can be determined from two
or more differently exposed images
by applying linear regression to the joint histogram, J12,
of the images, I1 and I2.
When two
successive frames of a video sequence are related through a group-action
that is near the identity of the group, one may think of the Lie
algebra of the group as providing the structure locally, so that
(7) may be solved as follows:
From (8)
we have that the (generalized) brightness change constraint
equation [28] is:
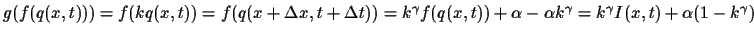 ,
where
I(x,t)=f(q(x,t)).
Combining this equation with the Taylor series
representation:
,
where
I(x,t)=f(q(x,t)).
Combining this equation with the Taylor series
representation:
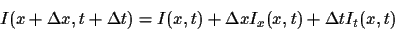 |
(10) |
where
Ix(x,t) = (df/dq)(dq(x)/dx), at time t,
and It(x,t) is the frame difference of adjacent frames,
we have:
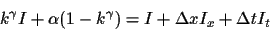 |
(11) |
Thus, the brightness change constraint equation becomes:
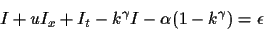 |
(12) |
where, normalizing,
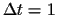 .
.



Next: Estimating in the the
Up: Lookpainting: Towards developing a
Previous: Mathematical framework for lookpainting:
Steve Mann
1999-04-11
![]() is equivalent to applying gamma correction
is equivalent to applying gamma correction
![]() to f in order to obtain
to f in order to obtain
![]() ,
where
,
where ![]() is typically between 0 and 1/2.
Note that when tonally registering images using this gamma correction,
one makes an implicit assumption that f(q) does not go all
the way to zero when q=0.
Thus a better model is
f=exp((1+qb)c) which also nicely captures the toe and shoulder of the
response function.
is typically between 0 and 1/2.
Note that when tonally registering images using this gamma correction,
one makes an implicit assumption that f(q) does not go all
the way to zero when q=0.
Thus a better model is
f=exp((1+qb)c) which also nicely captures the toe and shoulder of the
response function.
![]() ,
where
I(x,t)=f(q(x,t)).
Combining this equation with the Taylor series
representation:
,
where
I(x,t)=f(q(x,t)).
Combining this equation with the Taylor series
representation: