


Next: Parametric methods
Up: Lookpainting: Towards developing a
Previous: Building environment maps by
The mathematical framework for determining the unknown nonlinear
respose of a camera from nothing more than a collection of
differently exposed images, as well as a means of extending dymanic
range by combining differently exposed images was first published
in 1993[14]. This framework is now described in detail.
A set of functions,
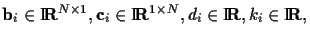 |
|
|
(1) |
is known as a projective-Wyckoff
set [12][13][4].
When N=2,
the projective-Wyckoff set
describes, within a common region of support,
a set of images, Ii, where
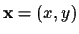 is the continuous spatial coordinate of
the focal plane of an
electronic imaging array or
piece of film, q is the quantity of light falling on the
sensor array, and f is the unknown nonlinearity of the camera's response
function (assumed to be invariant to
is the continuous spatial coordinate of
the focal plane of an
electronic imaging array or
piece of film, q is the quantity of light falling on the
sensor array, and f is the unknown nonlinearity of the camera's response
function (assumed to be invariant to 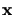 ).
In this case, the constants
).
In this case, the constants 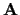 ,
,
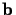 ,
,
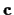 ,
and dare the parameters of a projective spatial coordinate transformation,
and the scalar parameter k is the parameter of a tonal transformation
(arising from a change in exposure from one image to the next).
In particular, the constant
,
and dare the parameters of a projective spatial coordinate transformation,
and the scalar parameter k is the parameter of a tonal transformation
(arising from a change in exposure from one image to the next).
In particular, the constant
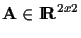 effects a linear coordinate transformation
of the image. (This constant represents the linear
scale of the image, as might compensate for various zoom
settings of a camera lens, rotation of the image, and image shear).
The constant
effects a linear coordinate transformation
of the image. (This constant represents the linear
scale of the image, as might compensate for various zoom
settings of a camera lens, rotation of the image, and image shear).
The constant
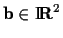 effects translation of the image,
and the constant
effects translation of the image,
and the constant
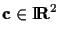 effects ``chirping'' of the image.
The constants
effects ``chirping'' of the image.
The constants 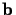 and
and 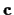 may each be regarded as a vector
with direction and magnitude (e.g. translation magnitude and direction,
as well as chirp rate and chirp direction).
may each be regarded as a vector
with direction and magnitude (e.g. translation magnitude and direction,
as well as chirp rate and chirp direction).
Methods of simultaneously estimating
the parameters of this relationship (1)
between images having a common region
of support, allowing the parameters, 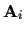 ,
,
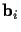 ,
,
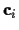 ,
di, and ki, as well as the function f, to be determined
from the images themselves, have been
proposed [14][13][12][4].
An outline of these methods follows, together with some new results.
The method presented in this paper
differs from that of [14] in that
the method presented here emphasizes the operation near the
neighbourhood of the identity (e.g. the ``video orbit'').
,
di, and ki, as well as the function f, to be determined
from the images themselves, have been
proposed [14][13][12][4].
An outline of these methods follows, together with some new results.
The method presented in this paper
differs from that of [14] in that
the method presented here emphasizes the operation near the
neighbourhood of the identity (e.g. the ``video orbit'').
For simplicity of illustration, let us consider the case for which
N=1 (e.g. so that pictures are functions of a single real variable).
In actual practice, N=2, but the derivation will be more illustrative
with N=1, in which case,
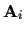 ,
,
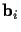 ,
,
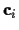 ,
di, and ki, are all
scalar quantities, and will thus be denoted
ai, bi, ci, di, and ki respectively.
,
di, and ki, are all
scalar quantities, and will thus be denoted
ai, bi, ci, di, and ki respectively.
For simplicity of illustration (without loss of generality), also
suppose that the projective-Wyckoff set contains two pictures,
I1=f(q) and
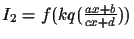 ,
where I2, called the comparison frame,
is expressed in the coordinates of I1, called the reference frame.
Implicit in this change of coordinates is the notion of an underlying
group representation for the projective-Wyckoff operator,
p12 which maps I2 as close as possible to I1, modulo
cropping at the edges of the frame, saturation or cutoff
at the limits of exposure, and noise (sensor noise, quantization noise, etc):
,
where I2, called the comparison frame,
is expressed in the coordinates of I1, called the reference frame.
Implicit in this change of coordinates is the notion of an underlying
group representation for the projective-Wyckoff operator,
p12 which maps I2 as close as possible to I1, modulo
cropping at the edges of the frame, saturation or cutoff
at the limits of exposure, and noise (sensor noise, quantization noise, etc):
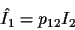 |
(2) |
where 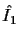 is the best approximation to I1 that can be generated
from I2.
is the best approximation to I1 that can be generated
from I2.
A suitable group representation is given by:
![\begin{displaymath}p_{a,b,c,d,k} =
\left[
\begin{array}{ccc}
a&b&0\\
c&d&0\\
0&0&k
\end{array} \right]
\end{displaymath}](img27.gif) |
(3) |
Thus, using the group representation (3),
we may rewrite
the coordinate transformation from any frame to any other, as
a composition of pairwise coordinate transformations.
For example, to obtain an estimate of image frame I1from any image, say, In, we observe:
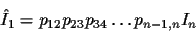 |
(4) |
where pi-1,i is the coordinate transformation from image
frame Ii to image Ii-1. The group representation (3)
provides a law of composition for these coordinate transformation operators,
so that it is never necessary to resample an image more than once.
Photographic film was traditionally characterized
by the so-called ``Density versus log Exposure'' characteristic
curve [15][16].
Similarly, for the CCD sensor arrays typically concealed in the sunglass-based
Reality Mediators,
logarithmic exposure units, 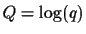 ,
may also be used,
so that one image will be
K = log(k) units darker than the other:
,
may also be used,
so that one image will be
K = log(k) units darker than the other:
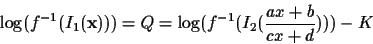 |
(5) |
where the difference in exposure, K, arises from the fact that
the camera will have an automatic exposure control of sorts, so that,
while looking around, darker or lighter objects will be included in the
region of the image which causes a global change in exposure.
The existence of an inverse for f follows from
the semi-monotonicity assumption.
Semi-monotonicity follows from the fact that we
expect![[*]](http://www.eecg.toronto.edu/GIF/latex2html_icons/foot_motif.gif) pixel values to either increase or stay the same with increasing quantity of
illumination, q.
This is not to suggest that the image content is semi-monotonic, but,
rather, that the response of the camera is semi-monotonic.
The semi-monotonicity assumption thus applies to the images after they
have been registered (aligned) by a spatial coordinate transformation.
pixel values to either increase or stay the same with increasing quantity of
illumination, q.
This is not to suggest that the image content is semi-monotonic, but,
rather, that the response of the camera is semi-monotonic.
The semi-monotonicity assumption thus applies to the images after they
have been registered (aligned) by a spatial coordinate transformation.
Since the logarithm function is also monotonic,
the problem comes down to estimating the semi-monotonic function
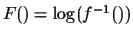 and the
parameters a,b,c,d, and
K = log(k),
given two pictures I1 and I2:
and the
parameters a,b,c,d, and
K = log(k),
given two pictures I1 and I2:
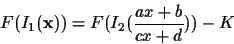 |
(6) |
Rather than solve for F, it has been found that registering
images to one reference image is more numerically robust [4].
In particular, this is accomplished through an operation of the form:
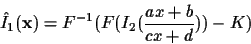 |
(7) |
which provides a recipe for spatiotonally registering
the second image with respect to the first
(e.g. appropriately lightening or darkening the second image to make
it have, apart from the effects of noise -- quantization noise, additive
noise, etc. -- the same tonal values as the first image, while at
the same time ``dechirping'' it with respect to the first).
This process of ``registering''
the second image with the first differs from
the image registration procedure commonly used
in much of image-based
rendering [17][18][19],
machine vision [20][21][22][23]
and image resolution
enhancement [24][11][25][26]
because it operates on both the domain
and the range,
 ,
(tonal range)
of the image
,
(tonal range)
of the image
 as opposed to just its domain (spatial coordinates)
as opposed to just its domain (spatial coordinates)
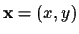 .
Image processing done on range-registered images is also related to the
notion of nonlinear mean filters [27],
and range-registration, as well as other forms of range-based processing
are also of special interest. Whether processing in a range-registered
function space, or processing quantigraphically[4],
it is often useful to consider the relationship between two differently
exposed images[14].
.
Image processing done on range-registered images is also related to the
notion of nonlinear mean filters [27],
and range-registration, as well as other forms of range-based processing
are also of special interest. Whether processing in a range-registered
function space, or processing quantigraphically[4],
it is often useful to consider the relationship between two differently
exposed images[14].
Proposition 3.1
When a function f(q) is monotonic, the
parametric plot
(f(q),f(kq)) can be expressed
as a function g(f) not involving q.
Definition 3.1
The resulting plot
(
f,
g(
f)) = (
f(
q),
f(
kq)) is called the
range-range plot [
12].
The function g is called the range-range function,
since it expresses the range of the function f(kq)as a function of the range of the function f(q),
and is independent of the domain, q, of the function f(q).
Separating the estimation process into two stages also allows us
a more direct route to ``registering'' the image ranges,
if for example, we do not need to know f, but only
require a recipe for expressing the range of f(kq) in
the units of f(q).
The determination of the function g(or f) can be done separately from
the determination of the parameters 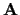 ,
,
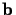 ,
,
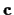 ,
d, and k.
The determination of g is typically done by comparing a variety
of images differing only in exposure. The function gis thus parameterized by the exposure k, and for a given camera,
the camera's response function is characterized by a family of
curves gi, one for each possible ki value, as illustrated in
Fig 10.
,
d, and k.
The determination of g is typically done by comparing a variety
of images differing only in exposure. The function gis thus parameterized by the exposure k, and for a given camera,
the camera's response function is characterized by a family of
curves gi, one for each possible ki value, as illustrated in
Fig 10.
Figure 10:
The family of range-range curves, gi for various values of ki capture the unique nonlinear response of the particular camera
under test (a 1/3 inch CCD array concealed inside eyeglasses
as part of a reality mediator, together with control unit).
The form of this curve may be determined from
two or more pictures that differ only in exposure.
(a) Curves as determined experimentally from pairs of
differently exposed pictures. (b) Curves as provided by
a one-parameter model, for various values of the parameter.
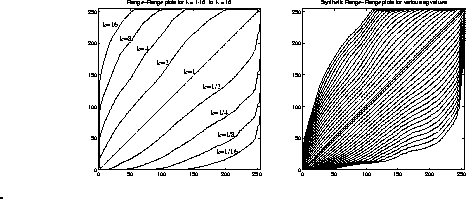 |
These curves are found by slenderizing the joint histogram
between images that differ only in exposure (each such image pair
determines a curve g for the particular k value corresponding
to the ratio of the exposures of the two images).
The slenderizing of the joint histogram amounts to
a non-parametric curve fit, and is what gives rise
to the determination of g.
The above method allows us to estimate, to within a constant
scale factor, the
continuous (unquantized) response function of the camera
without making any assumptions on the form of f, other
than semi-monotonicity.



Next: Parametric methods
Up: Lookpainting: Towards developing a
Previous: Building environment maps by
Steve Mann
1999-04-11
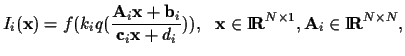
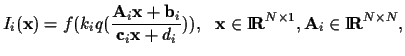
![]() ,
,
![]() ,
,
![]() ,
di, and ki, as well as the function f, to be determined
from the images themselves, have been
proposed [14][13][12][4].
An outline of these methods follows, together with some new results.
The method presented in this paper
differs from that of [14] in that
the method presented here emphasizes the operation near the
neighbourhood of the identity (e.g. the ``video orbit'').
,
di, and ki, as well as the function f, to be determined
from the images themselves, have been
proposed [14][13][12][4].
An outline of these methods follows, together with some new results.
The method presented in this paper
differs from that of [14] in that
the method presented here emphasizes the operation near the
neighbourhood of the identity (e.g. the ``video orbit'').
![]() ,
,
![]() ,
,
![]() ,
di, and ki, are all
scalar quantities, and will thus be denoted
ai, bi, ci, di, and ki respectively.
,
di, and ki, are all
scalar quantities, and will thus be denoted
ai, bi, ci, di, and ki respectively.
![]() ,
where I2, called the comparison frame,
is expressed in the coordinates of I1, called the reference frame.
Implicit in this change of coordinates is the notion of an underlying
group representation for the projective-Wyckoff operator,
p12 which maps I2 as close as possible to I1, modulo
cropping at the edges of the frame, saturation or cutoff
at the limits of exposure, and noise (sensor noise, quantization noise, etc):
,
where I2, called the comparison frame,
is expressed in the coordinates of I1, called the reference frame.
Implicit in this change of coordinates is the notion of an underlying
group representation for the projective-Wyckoff operator,
p12 which maps I2 as close as possible to I1, modulo
cropping at the edges of the frame, saturation or cutoff
at the limits of exposure, and noise (sensor noise, quantization noise, etc):
![]() ,
may also be used,
so that one image will be
K = log(k) units darker than the other:
,
may also be used,
so that one image will be
K = log(k) units darker than the other:
![]() pixel values to either increase or stay the same with increasing quantity of
illumination, q.
This is not to suggest that the image content is semi-monotonic, but,
rather, that the response of the camera is semi-monotonic.
The semi-monotonicity assumption thus applies to the images after they
have been registered (aligned) by a spatial coordinate transformation.
pixel values to either increase or stay the same with increasing quantity of
illumination, q.
This is not to suggest that the image content is semi-monotonic, but,
rather, that the response of the camera is semi-monotonic.
The semi-monotonicity assumption thus applies to the images after they
have been registered (aligned) by a spatial coordinate transformation.
![]() and the
parameters a,b,c,d, and
K = log(k),
given two pictures I1 and I2:
and the
parameters a,b,c,d, and
K = log(k),
given two pictures I1 and I2:
![]() ,
,
![]() ,
,
![]() ,
d, and k.
The determination of g is typically done by comparing a variety
of images differing only in exposure. The function gis thus parameterized by the exposure k, and for a given camera,
the camera's response function is characterized by a family of
curves gi, one for each possible ki value, as illustrated in
Fig 10.
,
d, and k.
The determination of g is typically done by comparing a variety
of images differing only in exposure. The function gis thus parameterized by the exposure k, and for a given camera,
the camera's response function is characterized by a family of
curves gi, one for each possible ki value, as illustrated in
Fig 10.
