


Next: Automatic generation of photo
Up: Lookpainting: Towards developing a
Previous: Parametric methods
The procedure for determining the coordinate transformation
is a repetitive procedure in which, for each
image pair, first an estimate is made
of the parameters of an approximate model of the transformation
going from one image to the other,
and then the corresponding parameters of the actual (``exact'')
transformation are determined from those of the approximate model.
The parameters of the ``exact'' model are then used to transform
one of the images in a first attempt to register it with the other image.
The registered images should, ideally, be identical within their region
of common support (overlap), but, there will in practice be some
residual error. Thus the process is repeated each time,
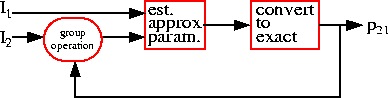
in order to reduce the error, as depicted in Fig 11
Figure:
Diagram depicting the ``lookpainting'' algorithm:
parameters are estimated from pairwise successive image frames,
such as I1 and I2 in the image sequence Ii. An approximate model that operates
in the neighbourhood of the identity may be used, and converted
to the actual (``exact'') model. As a result of the feedback
loop, the parameters of the exact model p21 relating images
I1 and I2 are estimated. Although this method involves
repeated estimation of the parameters, it should be noted that
it has advantages over the method presented
in [25][26] in the
sense that the estimation of the approximate parameters
is non-iterative. It should thus be emphasized that the
estimation process each time around the loop is direct
(non-iterative).
 |
In this way, the approximate model operates in the feedforward path,
and the exact model is implemented by way of the feedback path.
It should be noted that cumulative applications of coordinate
transformations (e.g. coordinate transformations of coordinate
transformations) are not done, but, rather, the group structure
and its law of composition are used so that there is only one
composite coordinate transformation done each time.
The approximate model used for the spatial coordinate transformation
is that of a quadratic Taylor series of the projective coordinate
transformation.
Substitution of the approximate model
into (12) gives:
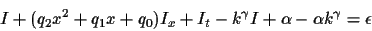 |
(13) |
where
q2=(bc/d2-a/d)c/d,
q1=a/d-bc/d2, and q0=b/d.
Minimizing
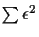 yields a linear
system of equations from which the values of the parameters can
be easily solved:
yields a linear
system of equations from which the values of the parameters can
be easily solved:
![$\displaystyle - \!
\left[ \! \!
\begin{array}{c} \sum x^2 I_x(I+I_t) \\
\sum x...
..._x(I+I_t) \\
\sum I(I+I_t) \\
\sum (I+I_t)
\end{array} \! \! \!
\right] \! \!$](img56.gif) |
|
|
(14) |
where
I(x,t)=f(q(x)) at time t,
Ix(x,t) = (df/dq)(dq(x)/dx), at time t,
and It(x,t) is the frame difference of adjacent frames.
The physical interpretation of k is the gain, and that
of 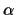 is the bias. These two constants amount to approximating
g with an affine relation (e.g. the plot of g with
a best-fit straight line), which is equivalent to approximating fwith a power law (Prop 3.2).
is the bias. These two constants amount to approximating
g with an affine relation (e.g. the plot of g with
a best-fit straight line), which is equivalent to approximating fwith a power law (Prop 3.2).
It should be noted that the parameters of the projective
coordinate transformation are determined indirectly,
assuming that 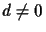 .
The condition for which d=0 corresponds to two successive
pictures where the optical axis of the camera had turned through
a right angle. That is, if one picture is taken, and then
the camera is rotated so it is pointing in
a direction 90 degrees from the direction in which it was
pointing during the taking of the first picture.
.
The condition for which d=0 corresponds to two successive
pictures where the optical axis of the camera had turned through
a right angle. That is, if one picture is taken, and then
the camera is rotated so it is pointing in
a direction 90 degrees from the direction in which it was
pointing during the taking of the first picture.
Since it is very difficult to turn the head a full 90 degrees
in the time between capture of two successive frames (1/60 second),
especially given the tendency of the apparatus to make one feel dizzy
and nauseated with such rapid changes in
motion![[*]](http://www.eecg.toronto.edu/GIF/latex2html_icons/foot_motif.gif) ,
it is sufficient to rule
out the d=0 possibility.
,
it is sufficient to rule
out the d=0 possibility.
Another way in which the algorithm might fail, is if the
images are not close enough to being in the same orbit of
the projective group of coordinate transformations.
Thus an underlying assumption of the method is that the wearer can
generate most of the image motion by
turning his/her head much more quickly than the lesser motion
produced by either scene motion or change of center of projection
(e.g. that head turning is faster than appreciably moving the body
from one location to another).
Once the parameters of the projective coordinate transformation,
as well as the parameters of the response curves relating the images
are found, (e.g. once all the unknowns, (bc-a)c, a-bc, b,
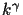 ,
and
,
and
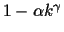 are found)
then the view into the
environment map is rendered from the
entire set of images which have overlapping
scene content, weighted by their certainty functions, as follows:
are found)
then the view into the
environment map is rendered from the
entire set of images which have overlapping
scene content, weighted by their certainty functions, as follows:
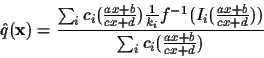 |
(15) |
Then the desired rendered view, constructed from the estimate q is given by:
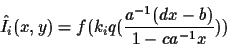 |
(16) |
An example of rendering
 from each of the frames I0 through I9 of the
``cluttered and unsafe fire-exit'' sequence
(original input data shown in Fig 12)
from each of the frames I0 through I9 of the
``cluttered and unsafe fire-exit'' sequence
(original input data shown in Fig 12)
Figure 12:
Ten images from the `cluttered and unsafe fire-exit'
investigative journalism sequence (taken using a
covert eyeglass-based system in which the camera had
automatic exposure).
As the camera pans across to take in more of the
open doorway, the image brightens up showing more of the
interior, while, at the same time, clipping highlight detail.
 |
is illustrated by way of
Fig 13.
Figure 13:
All images in the ``cluttered and unsafe fire-exit''
sequence expressed in the
spatiotonal coordinates of the first image in the sequence.
Note both the ``keystoning'', or ``chirping'' of the images
toward the end of the sequence, indicating the spatial
coordinate transformation, as well as the darkening of
the lighter images,
indicating the tone scale adjustment, both of which make
the images match (a).
Prior to quantization for printing in this figure,
the darker images (e.g. (i) and (j)) contained a tremendous
deal of shadow detail, owing to the fact that the quantization
step sizes are much smaller when compressed into the domain
of image (a).
![\begin{figure*}\centerline{ \vbox{
\vspace{0.10in}
\hbox{
\makebox[1.2in][c]{...
...[1.2in]{~(h)} \makebox[1.2in]{~(i)} \makebox[1.2in]{~(j)} }
} }
\end{figure*}](img64.gif) |
In particular, the process of rendering 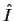 for any
value of A, b, c, and k, may be explored interactively on a computer
system, as illustrated in (Fig 14).
for any
value of A, b, c, and k, may be explored interactively on a computer
system, as illustrated in (Fig 14).
Figure 14:
VirtualCamera for Covert Telepresence:
Differently exposed pictures were generated by the natural
process of looking around.
(See Fig 12.)
These input images
were spatiotonally registered and combined into an environment
map of extremely high dynamic range which could then
be rendered, and
interactively explored in both its spatial domain
and its tonal range. (b) Here we are able to see a
white note left on a door upon which direct sunlight was
incident, while at the same time we can see all the way
down into a cluttered and unlit corridor to observe
an unsafe fire exit. Needless to say, the management of
this department store would not have responded favorably to
a traditional photographic camera, yet the image captured here
matches or exceeds
the quality that would have been attainable by professional
camera and lighting crews.
![\begin{figure*}\centerline{ \vbox{
\hbox{
\makebox[\colw][l]{\psfig{figure=/ma...
...lw}}
} \hbox{\makebox[\colw]{~(a)} \makebox[\colw]{~(b)} }
} }
\end{figure*}](img66.gif) |
This process turns the personal imaging apparatus into
a telematic camera in which viewers on the World Wide Web
experience something similar to
a QuickTime VR environment map [29],
except with some new additional controls allowing viewers
to move around in the environment map both spatially and tonally.
It should be emphasized that the environment map was generated by
images obtained
from a covert wearable apparatus, simply by looking around, and that
no special tripod or the like was needed, nor was there significant
conscious thought or effort required. In contrast to this
proposed method of building environment maps, consider what must
be done to build an environment map using QuickTime VR:
Despite more than twenty years photographic experience,
Charbonneau needed to learn new approaches for this
type of photography.
First, a special tripod rig is required,
as the camera must be completely level for all shots. A 35 mm camera ...
with a lens wider than 28 mm is best, and the camera should be
set vertically instead of horizontally on the tripod.
...
Exposure is another key element.
Blending together later will be difficult unless
identical exposure is used for all views. [29]
The constraint of the QuickTime VR method and many other methods
reported in the literature [30][31][32],
that all pictures be taken with identical exposure,
is undesirable for the following reasons:
-
Imposing that all pictures be taken with the same exposure
means that those images shot in bright areas of the scene will be
grossly overexposed, while those shot in dark areas will be
grossly underexposed. Normally the AGC would solve this
problem and adjust the exposure as the camera pans around the
scene, but since it must be shut off when using
previously existing methods, shooting all the pictures at
the same exposure will mean that most scenes will not record
well. Thus special studio lighting is often required
to carefully ensure that everything in the scene is equally
illuminated.
- It does not benefit from the advantages of the Wyckoff principle
of combining differently exposed images.
In contrast to the prior art,
the proposed method allows natural scenes of extremely high dynamic
range to be captured from a
covert eyeglass-based Reality-Mediator, by
simply looking around.
The natural AGC of the camera ensures that (1) the camera will
adjust itself to correctly expose various areas of the scene,
so that no matter how bright or dark (within a very large range)
objects in the scene are, they will be properly represented in at least some
of the input images, and (2) the natural ebb and flow of the gain,
as it tends to fluctuate, will ensure that there is a great deal
of overlapping scene content that is differently exposed, and
thus the same quantities of light
from each direction in space will be
measured with a large variety of different exposures.
In this way,
it will not be necessary to deliberately shoot at different apertures
in order to obtain the Wyckoff effect.



Next: Automatic generation of photo
Up: Lookpainting: Towards developing a
Previous: Parametric methods
Steve Mann
1999-04-11


![]() yields a linear
system of equations from which the values of the parameters can
be easily solved:
yields a linear
system of equations from which the values of the parameters can
be easily solved:
![$\displaystyle \left[ \!
\begin{array}{ccccc}
\! \! \sum x^4I_x^2 &\!\!\!\! \sum...
.../d^2 \\
b/d\\
k^\gamma\\
1-\alpha k^\gamma
\end{array} \!
\right] \! \! \!
=$](img55.gif)
![$\displaystyle - \!
\left[ \! \!
\begin{array}{c} \sum x^2 I_x(I+I_t) \\
\sum x...
..._x(I+I_t) \\
\sum I(I+I_t) \\
\sum (I+I_t)
\end{array} \! \! \!
\right] \! \!$](img56.gif)
![]() .
The condition for which d=0 corresponds to two successive
pictures where the optical axis of the camera had turned through
a right angle. That is, if one picture is taken, and then
the camera is rotated so it is pointing in
a direction 90 degrees from the direction in which it was
pointing during the taking of the first picture.
.
The condition for which d=0 corresponds to two successive
pictures where the optical axis of the camera had turned through
a right angle. That is, if one picture is taken, and then
the camera is rotated so it is pointing in
a direction 90 degrees from the direction in which it was
pointing during the taking of the first picture.
![]() ,
it is sufficient to rule
out the d=0 possibility.
,
it is sufficient to rule
out the d=0 possibility.
![]() ,
and
,
and
![]() are found)
then the view into the
environment map is rendered from the
entire set of images which have overlapping
scene content, weighted by their certainty functions, as follows:
are found)
then the view into the
environment map is rendered from the
entire set of images which have overlapping
scene content, weighted by their certainty functions, as follows:
![]() from each of the frames I0 through I9 of the
``cluttered and unsafe fire-exit'' sequence
(original input data shown in Fig 12)
from each of the frames I0 through I9 of the
``cluttered and unsafe fire-exit'' sequence
(original input data shown in Fig 12)

![\begin{figure*}\centerline{ \vbox{
\vspace{0.10in}
\hbox{
\makebox[1.2in][c]{...
...[1.2in]{~(h)} \makebox[1.2in]{~(i)} \makebox[1.2in]{~(j)} }
} }
\end{figure*}](img64.gif)
![\begin{figure*}\centerline{ \vbox{
\hbox{
\makebox[\colw][l]{\psfig{figure=/ma...
...lw}}
} \hbox{\makebox[\colw]{~(a)} \makebox[\colw]{~(b)} }
} }
\end{figure*}](img66.gif)