ECE 431F, (DSP) MIDTERM TEST

October 18, 2000, 6:15PM to 7:45PM

Time allowed: 90 minutes. Closed book. 3 problems (9+9+7 = 25points)

Problem 1 (3+3+3=total 9 points)

A street has four kinds of traffic, comprised of: An ideal traffic control radar illuminates the roadway with a high frequency signal for speed measurement. For simplicity, assume that any traffic that is moving moves in the same direction toward the radar, and that a return signal, which you have been asked to analyze, has some or all of only the following exact frequencies present:
(a) (3points) The Department of Transportation asks you to purchase a sampler from a catalog of ideal data capture samplers, with sampling frequencies available from 1 kHz (1,000 Hz) to 100 gigaHertz (100,000,000,000 Hz), available in 1 kHz steps. Since there is increasing cost for increasing frequency, you are asked to propose the minimum such sampling frequency, $F_s$, required in order to avoid irrecoverable aliasing in the return signal, $g(t) = c_0 g_0(t) + c_1 g_1(t) + c_2 g_2(t) + c_3 g_3(t)$ for arbitrary constants $c_0$, $c_1$, $c_2$, and $c_3$. Explain your reasoning for this choice.
ANSWER: Choose a 4kHz sampler.
Reasoning: There is no irrecoverable aliasing when sampled at 4kHz. If you chose 3kHz, you were wrong, because you would not be able to distinguish type 3 traffic from type 0 traffic. If you chose some really high frequency on the order of 60,000,000,000 and then some, you were probably not listening in class when we covered sampling of bandpass signals, and recoverable "aliasing" of bandpass signals.

If you correctly understood aliasing, e.g. that sampling in time introduces periodicity in frequency (a replication of the signal over and over again in frequency), etc., you probably correctly answered this question.

(b) (3points) Assume that you have a sequence of numbers $g[n] = g(nT_s)$, where $T_s = 1/F_s$ (where $F_s$ is that which you selected above). Propose a method of discrete time signal processing in order to determine the constants $c_0$, $c_1$, $c_2$, and $c_3$ present in the original signal $g(t)$, by way of discrete time processing of $g[n]$. Explain your method.

ANSWER: A simple method is to take four samples (e.g. sample for 1 millisecond at 4kHz) and then take the four point DFT of those samples. The coefficients of the DFT would give you the constants.
(c) (3points) Assuming the minimum sampling frequency you chose for $F_s$, what is the minimum number of uniformly spaced samples of $g(t)$ required to determine the constants $c_0$, $c_1$, $c_2$, and $c_3$. Explain your reasoning.
ANSWER: You need at least four points. Given the choice of integer multiples of 1kHz sampling rates (e.g. 0kHz, 1kHz, 2kHz, 3kHz, 4kHz, 5kHz, etc.), specified in the problem statement, sampling for 1 millisecond at 4kHz will provide sufficient degrees of freedom to solve the problem. Any more points taken are excess. (Since this is an idealiased problem, there is no need to signal average over a long time interval.)

Problem 2 (3+3+3=total 9 points)

Ham radio station N1NLF-1 is capable of operating in four possible modes, transmitting at: Two ideal point source antennas, located $d=40m$ apart are directly in line of sight of a listening post and monitoring station equipped with a sampler (SAMPLER) on the rooftop of a building as shown in the figure below.

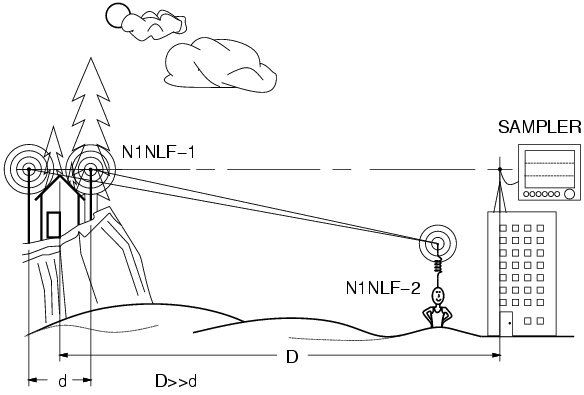
Assume that the same signal is fed to both antennas, and that the signal received from each antenna has equal strength (e.g. $D>>d$), and that linearity and superposition applies to the received signal from each.

The sampler coherently operates at one fixed frequency of 10 megasamples (10,000,000 samples) per second, and can acquire four complex--valued samples at a time.

It is known that station N1NLF-1 always transmits at the same frequency to a mobile station N1NLF-2 located at ground level.

The following four samples are measured at the listening post: 

   1.0000           -0.7071+ 0.7071i  -0.0000- 1.0000i   0.7071+ 0.7071i
where $i = \sqrt{-1}$. The four samples are known to be exactly $1$, $(-1+i)/\sqrt{2}$, $-i$, and $(1+i)/\sqrt{2}$. For simplicity, assume that no other interference, reflections, noise, or other imperfections exist in the system.

(a) (3points) Compute the four point DFT of the four samples given. Show your work and calculations in detail.

ANSWER:
four point DFT is: 
   1.0000+ 0.4142i   1.0000+ 2.4142i   1.0000- 2.4142i   1.0000- 0.4142i
It is expected that the student would show how these numbers were calculated (e.g. by way of summation, or by way of evaluating the DFT, or by just writing out the 4 by 4 matrix with the 16 entries, etc.).

(b) (3points) Compute the signal strength (e.g. magnitude squared) at each of the four values found in (a). Explain the intuitive physical significance of this set of four signal strengths. From these signal strengths, together with your knowledge of the situation, propose an hypothesis for what frequency or frequencies station N1NLF-1 could be transmitting at.

ANSWER:
discussion figure
four point DFT is: 
   1.0000+ 0.4142i   1.0000+ 2.4142i   1.0000- 2.4142i   1.0000- 0.4142i
absolute value is: 
    1.0824    2.6131    2.6131    1.0824
and thus, absolute value squared is: 
    1.1716    6.8284    6.8284    1.1716
The intuitive significance of these numbers is the energy or power present at each frequency bin of the DFT. Since we know that N1NLF-1 always transmits at the same frequency (e.g. it doesn't transmit at two different frequencies), we know that it must be transmitting midway between the two frequency bins above, since the two are both the same strength. Therefore, N1NLF-1 must be transmitting at a fractional frequency of 1.5/4 which is midway between fractional frequencies 1/4 and 2/4=1/2.

The fractional frequency of 1.5/4 = 0.3750 is an actual frequency of 10 MHz times 0.3750 which is 3.75 MHz or any of the aliases of 3.75 MHz, such as 13.75 MHz, 23.75 MHz, ... 443.75 MHz, etc.. Thus we must chose between the second and fourth modes of operation. We must rule out the second mode of operation (3.75 MHz) because that produces destructive interference, e.g. the signals are received equally from the two antennas, according to the problem statement, and these are 180 degrees out of phase (phase shift of 40 meters spacing for an 80 meters wavelength). Therefore we conclude that N1NLF-1 must have been transmitting at 443.75 MHz, the only alias of 3.75 MHz + 10n MHz that falls within the frequency range of 440 MHz to 450 MHz.

Note that this alias at 443.75 MHz is not an integer multiple of 3.75MHz, e.g. 

443.75/3.75 = 118.3333...
and therefore signals transmitting at 443.75 MHz will not give rise to destructive interference along the path in line with the two antennas.

(c) (3points) You are asked to present your findings at a board meeting, and would like to give a plausible explanation for a value midway between the two highest values you found in (b). Propose a method for determining a value midway between these two highest values, and explain why your method makes intuitive sense, within the context of discrete time signal processing. Use your method to calculate the value midway between the two highest values you found in (b).

ANSWER:
To interpolate in frequency, zeropad in time, and evaluate the 8 point DFT at the desired frequency, as shown in this figure. Of course you do not need to calculate all eight of the new samples (well you already calculated four of them anyway, but you still don't need to calculate all the remaining four, because you were not asked for them, and they're zero anyway). The magnitude squared of the one point of the 8 point DFT you were asked to calculate was 16.0000.

Problem 3 (7 points)

problem 4.60 from the course textbook

solution (figure)

ECE431 midterm 2000 LaTeX source file
ECE431 midterm 2000 PostScript print file