Sampling of cosines:
Aliasing as negative frequency:
Reordering into negative frequencies:
Similarly, if we desire, we can also shift the time origin to the center (e.g. in Matlab, we can use the fftshift() function in both time and frequency):
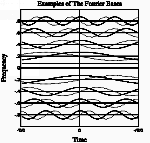
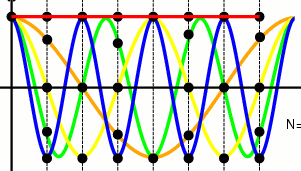
Sampling of cosines:

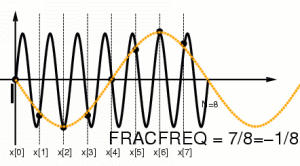
Aliasing as negative frequency:

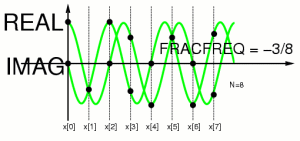
Reordering into negative frequencies:

Similarly, if we desire, we can also shift the time origin to the center
(e.g. in Matlab, we can use the fftshift() function in both time and
frequency):

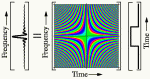
If we take enough of these sines and cosines, along rows of a large matrix,
e.g. for a 1024 point DFT, the cosines will make a 1024 by 1024 matrix,
and so will the sines. The central portion of a Fourier transform
matrix looks like this:
 (Real part)
(Real part)
 (Imag. part)
(Imag. part)
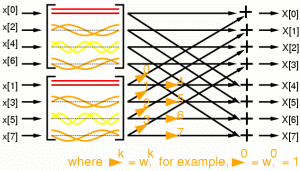
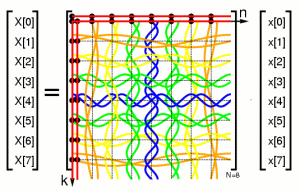
The Fourier Transform can be computed as a matrix multiplication:
The 8 point DFT as a matrix multiplication:
Separation into even and odd columns:
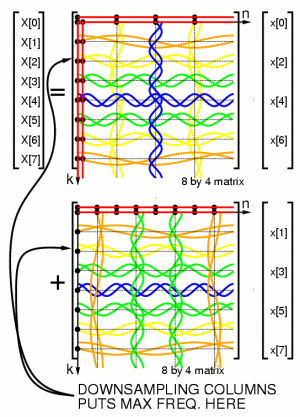
Separation into even and even columns:
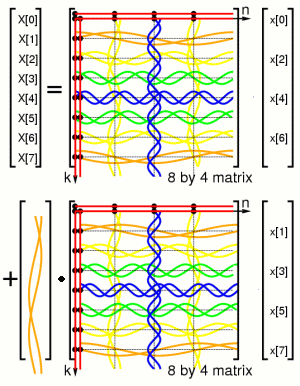
where the dot represents element by element (Hadamard) multiplication
(as would be denoted by ".*" if this were done in Matlab); the
dot will be omitted in the rest of this document, for simplicity,
where it is understood by dimensional consistency where it is assumed.
Decimation of columns by two gives aliasing:
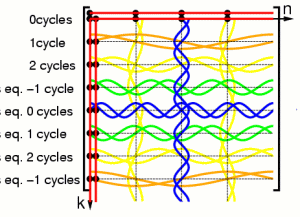
thus the matrix repeats twice in the up-down direction:
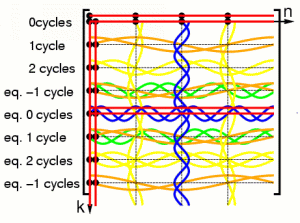
so that we can write the 8point fourier operator as two four point
fourier operators:
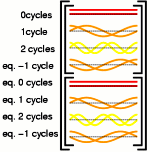
therefore the DFT of 8 points can be expressed as two 4 point DFTs:
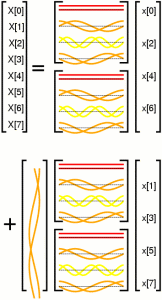
The above matrix equation can be implemented as a circuit:
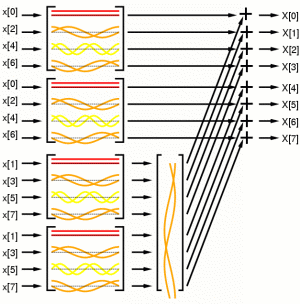
Redundant elements of the circuit can be deleted:
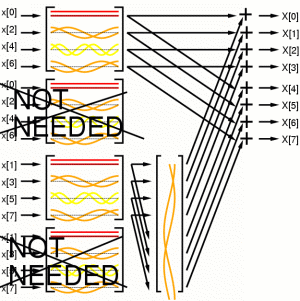
Thus decimation in time has simplified the circuit design: