The plots are like the cosine-only plots from before,
except that now we have both cosine and sine parts on each plot.
Here are the cosine (real, labelled "R") and sine (imaginary, labelled "I")
parts:
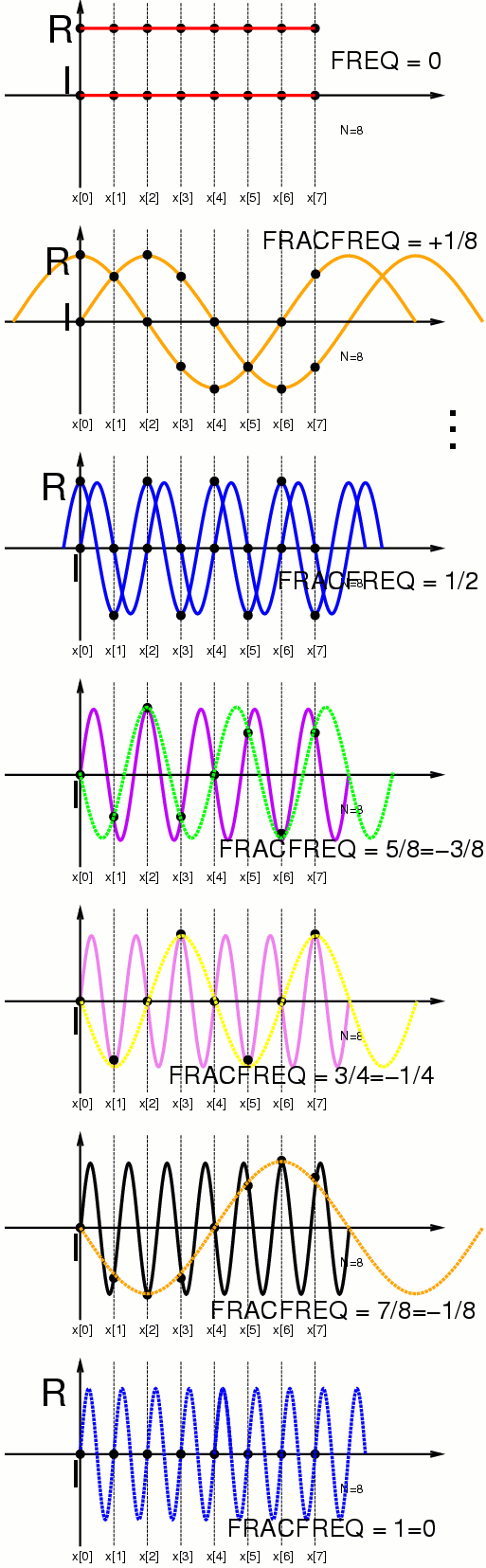
- The red plot shows zero cycles, i.e. cosine(0)=1, and sine(0)=0;
- The orange plot shows one cycle;
- ... (and so on...)
- The blue plot shows four cycles, right at the Nyquist frequency;
- The indigo colored plot shows five cycles of the sinewave,
and we see that the samples correspond exactly to an upside
down (or backwards)
sinewave having three cycles. We recall that the cosine
waves were the same for fractional frequency of +5/8 and +3/8,
but the sinewave corresponds only when upsidedown or backwards,
i.e. -sine(t)=sine(-t). The cosine part is symmetrical,
i.e. cosine(t)=cosine(-t), so we have, simply, that
the total 5Hz signal (both cosine and sine part), when played backwards,
has the same samples as a 3Hz signal. Playing backwards is for negative
frequency.
This means that +5Hz (indigo) has the same samples as -3Hz
(plotted in green);
- The purple (violet) colored plot shows six cycles of the sinewave.
Here we see that the +6Hz signal (violet)
has the same samples as a -2Hz signal (plotted in yellow).
- The ultraviolet colored (i.e. "black light colored") plot,
drawn in black, shows seven cycles of a sinewave.
When sampled at 8Hz, the 7Hz sinewave (black) has the same samples as
a -1Hz sinewave (plotted in orange).

