Consider the comparametric equation g=f2, having d.c. sol'n: log(f)=q, F=q, log(F)=Q.

Try running this in Octave, study it well, understand it fully, and then modify this script file to similarly understand various other examples, such as g=f+1, having d.c. sol'n f=log2(q), f=Q, and, try to understand, in this way, all the entries in Table 4.4 of the Intelligent Image Processing book, of which there are copies on reserve in the library that's on the second floor of Sandford Fleming building. Note that this example is just a simulacrum for the continuous world, and does not imply, of course, that there are only 1000 points per unit Q, because really there are infinity points per unit Q.

You should be able to write a closed-form mathematical expression for any portion of these various curves, or similar other examples, in terms of any of the plots.

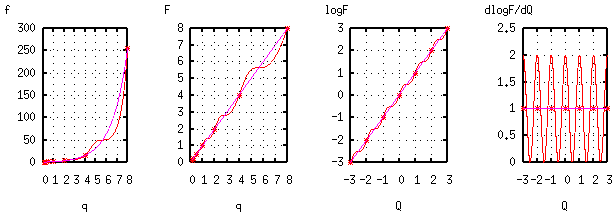
Here is the script, that also appears below: 

% consider g=f^2, having d.c. sol'n: log(f)=q, F=q, log(F)=Q.
Q=linspace(-3,3,6000);
q=2..^Q;
logF=1/2/pi*sin(2*pi*Q) + Q; % sine plus slope
F=2..^logF;
f=2..^F;
%% not used anywhere: F=log(f)/log(2);
grid
gset nokey
xlabel('q')
ylabel('f')
qintegers=[1/8 1/4 1/2 1 2 4 8];
fintegers=2..^qintegers;
ftrue=2..^q;
subplot(241);
axis(); % set axis to "normal"
plot(q,f,qintegers,fintegers,'+',qintegers,fintegers,"*",q,ftrue)

subplot(242);
xlabel('q')
ylabel('F')
Fintegers=qintegers;
Ftrue=q;
plot(q,F,qintegers,Fintegers,'+',qintegers,Fintegers,"*",q,Ftrue)
Qintegers=log(qintegers)/log(2);
subplot(243);
xlabel('Q')
ylabel('logF')
logFintegers=Qintegers;
logFtrue=Q;
plot(Q,logF,Qintegers,logFintegers,'+',Qintegers,logFintegers,"*",Q,logFtrue)
subplot(244); % Periodizer is dlogF/dQ
xlabel('Q')
ylabel('dlogF/dQ')
%%%axis([-3 3 -4 3])
Qt=Q(1:length(Q)-1); % Qtruncated
dlogFdQ=1000*diff(logF);
dlogFintegers=1*ones(size(Qintegers));
x=[-3 3]; y=[1 1];
plot(Qt,dlogFdQ,Qintegers,dlogFintegers,'+',Qintegers,dlogFintegers,'*',x,y)
subplot(111);

Also, don't forget to thoroughly study the last question on last year's final exam.