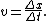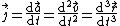Information about Derivatives Of Displacement
Position and its various derivatives define an ordered hierarchy of meaningful concepts. There are special names for the derivatives of position (first derivative is called velocity, second derivative is called acceleration, etc.), up to the eighth derivative and down to the -5th derivative (fifth integral).
These derivatives of position and their corresponding names and special significance are as follows:
0th derivative is position
In physics, displacement is the vector that specifies the change in position of a point, particle, or object. The position vector directs from the reference point to the present position.A sensor is said to be displacement-sensitive when it responds to absolute position.
For example, whereas a dynamic microphone is a velocity receiver (responds to the derivative of sound pressure or position), a carbon microphone is a displacement receiver in the sense that it responds to sound pressure or diaphragm position itself.
1st derivative is velocity
Velocity is defined as the rate of change of position or the rate of displacement. It is a vector physical quantity, both speed and direction are required to define it. In the SI (metric) system, it is measured in meters per second (m/s). The scalar absolute value (magnitude) of velocity is speed. For example, "5 metres per second" is a speed and not a vector, whereas "5 metres per second east" is a vector. The average velocity (v) of an object moving through a displacement (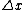 ) in a straight line during a time interval (
) in a straight line during a time interval (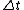 ) is described by the formula:
) is described by the formula:
Simply put, velocity is change in position per unit of time.
Most piano-style music keyboards are approximately velocity-sensitive, within a certain specific, though limited range of key travel, i.e. to a first-order approximation, a note is made louder by hitting a key faster. Most electronic music keyboards are also velocity sensitive, and measure the time interval between switch contact closures at two different positions of key travel on each key.
2nd derivative is acceleration
Acceleration is defined as the rate of change of velocity. It is thus a vector quantity with dimension length/time². In SI units, acceleration is measured in metres/second² (m·s-²). The term "acceleration" generally refers to the change in instantaneous velocity.3rd derivative is jerk
Jerk, (sometimes called jolt in British English, but less commonly so, due to possible confusion with use of the word to also mean electric shock), surge or lurch, is the rate of change of acceleration; more precisely, the derivative of acceleration with respect to time, the second derivative of velocity, or the third derivative of displacement. Jerk is described by the following equation: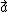 is acceleration,
is acceleration,
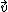 – velocity,
– velocity,
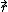 – position
– position
 stands for time.
stands for time.
4th derivative is jounce
Jounce (also known as snap) is the fourth derivative of the position vector with respect to time, with the first, second, and third derivatives being velocity, acceleration, and jerk, respectively; in other words, jounce is the rate of change of the jerk with respect to time.5th and beyond: Higher-order derivatives
Following jounce (snap), the fifth and sixth derivatives of the displacement vector are sometimes referred to as crackle and pop, respectively. The seventh and eighth derivatives of the displacement vector are occasionally referred to as lock and drop.-1st derivative (integral) of position is absement
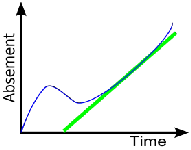
The
blue curve represents absement. The slope of the blue curve, at a
particular point, denotes position. Thus if the blue line denoted
quantity of water in a reservoir where flow was dicated linearly by
displacement of a control valve, the slope of the green line would give
the position of the control valve at that point in time.
The rate of change of absement is position. Absement is a quantity with dimension length*time. In SI units, absement is measured in metre seconds (m·s).
One meter-second corresponds to being absent from an origin or other reference point for a duration of one second. This amount of absement is equal to being two metres away from the origin for one half second, or being one half a metre from the origin for two seconds, or a 1mm absence for 1000 seconds, a 1km absence for 1 millisecond, etc..
The word "absement" is a blend of the words absence and displacement.
Useful applications of absement
Whereas most musical keyboard instruments, such as the piano, and many electronic keyboards, respond to velocity at which keys are struck, and some such as the tracker-organ, respond to displacement (how far down a key is pressed), flow-based musical instruments such as the hydraulophone, respond to the integral of displacement, i.e. to a time-distance product. Thus "pressing" a key (water jet) on a hydraulophone down for a longer period of time will result in a buildup of the sound level, as fluid (water) begins to fill the sounding mechanism (reservoir), up to a certain maximum filling point beyond which the sound levels off (along with a slow decay). Hydraulophone reservoirs have an approximate integrating effect on the distance or displacement applied by the musician's fingers to the "keys" (water jets). Whereas the piano provides more articulation and enunciation of individual note-onsets than the organ, the hydraulophone provides a more continuously fluidly varying sound than either the organ or piano.Of course all these models are approximate: hydraulophones are approximately presement-responsive, pianos are approximately velocity-responsive, etc..
The concepts of absement and presement originated in regards to flow-based musical instruments like hydraulophones, but may be applied to any area of physics, as they exist along the hierarchy of the derivatives of displacement.
A very slow-responding pipe-organ with tracker-action can often exhibit an effect similar to that of a hydraulophone, when it takes time for the wind and sound levels to build up, so that the sound level is approximately the product of how far down a key is pressed and how long it is held down for.
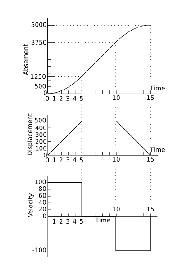
Example
to illustrate the concept of absement: Consider a 5-hour train ride
that takes you 500 miles directly from your home, in a straight line,
where you stay for 5 hours and then return. Suppose you want to stay
logged into your home computer at a communications cost of
$1/mile/hour(where "mile" is the distance between your current position
and your home). The total cost of your online communications is $5000,
since the absement (time-integral of displacement) is 5000 mile hours
(1250 mile hours on the way to your destination, plus 500 miles * 5
hours stay = 2500 mile hours, plus 1250 mile hours of absement during
the return trip).
As a crude but simple example, absement may be used, very approximately, to model the cost of a long-distance phone call as the product of distance and time. A short-duration call over a long distance might, for example, represent the same quantity of absement as a long-duration call over a shorter distance.
Absement may also be used in sociological studies, i.e. we might express loneliness or homesickness as a product of distance from home and time away from home. Simply put, the old aphorism "absence makes the heart grow fonder" has been expressed as "absement makes the heart grow fonder"[1], to suggest that it matters both how absent one is (i.e. how far), as well as for how long one is absent.
Absement versus presement
Absement refers to the time-distance product (or more precisely the integral of displacement) away from a reference point, whereas the integral of reciprocal position, called presement, refers to the closeness, compounded over time [1].The word "presement" is a portmanteau constructed from the words presence and displacement.
Placement (scalar quantity, nearness) is defined as the reciprocal of position (scalar quantity distance), and presement refers to the time-integral of placement. Most notably, with some high-pressure hydraulophones, it is physically impossible to fully obstruct a water jet, so position can never reach zero [1], and thus placement remains finite, as does its time integral, presement.
Simply put, absement is the time-integral of farness, and presement is the time-integral of nearness, to a given point (e.g. farness or nearness of a musicians finger to/from the exit port of a water jet in a hydraulophone).
Lower-order derivatives (higher-order integrals) of position
Some hydraulophones, such as the North Nessie (the hydraulophone on the North side of hydraulophone circle) at the Ontario Science Centre consist of cascaded hydraulophonic mechanisms, resulting in a double-integrating effect. In particular, the hydraulophone is linked indirectly to the North pipes, such that the water in direct physical contact with the fingers of the musician is not the same water in the organ pipes. As a result of this indirection, the instrument itself responds to presement/absement, the first integral of position whereas the pipes respond absemently to the action in the instrument, i.e. to the second integral of position of the player's fingers. The time-integral of the time-integral of position is called absity/presity.Absity is a portmanteau formed from the words absement (or absence) and velocity.
Following this pattern, higher integrals of displacement may be named as follows:
- Absement is the integral of displacement;
- Absity is the double integral of displacement;
- Abseleration is the triple integral of displacement;
- Abserk is the fourth integral of displacement;
- Absounce is the fifth integral of displacement, and so on...
Although there are no three-stage hydraulophones currently being manufactured as products, there are a number of three-stage (and some with higher numbers of stages) hydraulophone prototypes, in which some elements of the sound production respond to absity/presity, abseleration/preseleration, etc..
Summary
The following table is a summary of the derivatives of position:derivative terminology SI unit meaning -5 absounce m·s5 time integral of abserk -4 abserk m·s4 time integral of abseleration -3 abseleration m·s³ time integral of absity -2 absity m·s² time integral of absement -1 absement (absition) m·s time integral of position 0 position (displacement) m position 1 velocity m·s-1 rate-of-change of position 2 acceleration m·s-2 rate of change of velocity 3 jerk m·s-3 rate of change of acceleration 4 jounce (snap) m·s-4 rate of change of jerk 5 crackle m·s-5 rate of change of jounce 6 pop m·s-6 rate of change of crackle 7 lock m·s-7 rate of change of pop 8 drop m·s-8 rate of change of lock References
[1] What is the term used for the third derivative of position?
[2] Steve Mann, Ryan Janzen, Mark Post (2006), "Hydraulophone Design Considerations: Absement, Displacement, and Velocity-Sensitive Music Keyboard in which Each Key is a Water Jet." ACM Multimedia (MM 2006), pp. 519-528, Santa Barbara, CA, Oct. 23-27, 2006. ([1])
[3] Steve Mann, Michael Georgas, Ryan Janzen (2006), "Water jets as pixels: water fountains as both sensors and displays", Eighth IEEE International Symposium on Multimedia, IEEE ISM2006, pp. 766-772, Dec. 11-13, 2006, San Diego, CA.
[4] Steve Mann, Ryan Janzen, Raymond Lo, Chris Aimone (2007), "Inventing new instruments based on a computational "hack" to make a badly tuned or unpitched instrument play in perfect harmony", International Computer Music Conference, ICMC2007, Aug. 27-31, 2007, Copenhagen, Denmark.Position may refer to:- A location in a coordinate system, usually in two or more dimensions; the science of position and its generalizations is topology
..... Read more.Physics is the science of matter[1] and its motion[2][3], as well as space and time[4][5] —the science that deals with concepts such as force, energy, mass, and charge.
..... Read more.spatial vector, or simply vector, is a concept characterized by a magnitude and a direction. A vector can be thought of as an arrow in Euclidean space, drawn from an initial point A pointing to a terminal point B.
..... Read more.A velocity receiver is a sensor that responds to velocity rather than absolute position.
For example, dynamic microphones are velocity receivers.
Likewise, many electronic keyboards used for music are velocity sensitive, and may be said to posess a velocity receiver in each
..... Read more.A displacement receiver is a device that responds to or is sensitive to directed distance (displacement).
Examples of displacement receivers include carbon microphones, strain gauges, and pressure sensors or force sensors, which, to within an appropriate scale factor,
..... Read more.velocity is defined as the rate of change of position. It is a vector physical quantity, both speed and direction are required to define it. In the SI (metric) system, it is measured in meters per second (m/s). The scalar absolute value (magnitude) of velocity is speed.
..... Read more.derivative is a measurement of how a function changes when the values of its inputs change. Loosely speaking, a derivative can be thought of as how much a quantity is changing at some given point.
..... Read more.spatial vector, or simply vector, is a concept characterized by a magnitude and a direction. A vector can be thought of as an arrow in Euclidean space, drawn from an initial point A pointing to a terminal point B.
..... Read more.A physical quantity is either a physical property that can be measured (e.g. mass, volume, etc.), or the result of a measurement. The value of a physical quantity Q is expressed as the product of a numerical value and a physical unit [Q].
..... Read more.Si, si, or SI may refer to (all SI unless otherwise stated):
In language:- One of two Italian words:
- sì (accented) for "yes"
- si
..... Read more.Metre per second (U.S. spelling: meter per second) is an SI derived unit of both speed (scalar) and velocity (vector quantity which specifies both magnitude and a specific direction), defined by distance in metres divided by time in seconds.
..... Read more.scalar is a simple physical quantity that does not depend on direction, and is therefore not changed by coordinate system rotations (in Newtonian mechanics), or by Lorentz transformations (in relativity). (Contrast to vector.
..... Read more.In mathematics, the absolute value (or modulus[1]) of a real number is its numerical value without regard to its sign. So, for example, 3 is the absolute value of both 3 and −3.
..... Read more.For other senses of this word, see magnitude.
The magnitude of a mathematical object is its size: a property by which it can be larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which
..... Read more.Speed is the rate of motion, or equivalently the rate of change in position, many times expressed as distance d traveled per unit of time t.
Speed is a scalar quantity with dimensions distance/time; the equivalent vector quantity to speed is known as
..... Read more.acceleration is defined as the rate of change of velocity, or, equivalently, as the second derivative of position. It is thus a vector quantity with dimension length/time². In SI units, acceleration is measured in metres/second² (m·s-²).
..... Read more.derivative is a measurement of how a function changes when the values of its inputs change. Loosely speaking, a derivative can be thought of as how much a quantity is changing at some given point.
..... Read more.velocity is defined as the rate of change of position. It is a vector physical quantity, both speed and direction are required to define it. In the SI (metric) system, it is measured in meters per second (m/s). The scalar absolute value (magnitude) of velocity is speed.
..... Read more.spatial vector, or simply vector, is a concept characterized by a magnitude and a direction. A vector can be thought of as an arrow in Euclidean space, drawn from an initial point A pointing to a terminal point B.
..... Read more.Length is the long dimension of any object. The length of a thing is the distance between its ends, its linear extent as measured from end to end. This may be distinguished from height, which is vertical extent, and width or breadth
..... Read more.time.
One view is that time is part of the fundamental structure of the universe, a dimension in which events occur in sequence, and time itself is something that can be measured.
..... Read more.Si, si, or SI may refer to (all SI unless otherwise stated):
In language:- One of two Italian words:
- sì (accented) for "yes"
- si
..... Read more.The metre (or meter) per second squared is the SI derived unit of acceleration. It is a measure of magnitude and can be a scalar measure or, when associated with a direction, a vector, for example by having sign positive or negative.
..... Read more.jerk, jolt (esp in British English), surge or lurch, is the rate of change of acceleration; more precisely, the derivative of acceleration with respect to time, the second derivative of velocity, or the third derivative of position.
..... Read more.British English (BrE, BE, en-GB) is the broad term used to distinguish the forms of the English language used in the United Kingdom from forms used elsewhere in the Anglophone world.
..... Read more.acceleration is defined as the rate of change of velocity, or, equivalently, as the second derivative of position. It is thus a vector quantity with dimension length/time². In SI units, acceleration is measured in metres/second² (m·s-²).
..... Read more.derivative is a measurement of how a function changes when the values of its inputs change. Loosely speaking, a derivative can be thought of as how much a quantity is changing at some given point.
..... Read more.velocity is defined as the rate of change of position. It is a vector physical quantity, both speed and direction are required to define it. In the SI (metric) system, it is measured in meters per second (m/s). The scalar absolute value (magnitude) of velocity is speed.
..... Read more.In physics, displacement is the vector that specifies the position of a point or a particle in reference to an origin or to a previous position. The vector directs from the reference point to the current position.
..... Read more.acceleration is defined as the rate of change of velocity, or, equivalently, as the second derivative of position. It is thus a vector quantity with dimension length/time². In SI units, acceleration is measured in metres/second² (m·s-²).
..... Read more.